| Titel: | Adcock's Wasserhebmaschine in der Kohlengrube bei Pemperton.. |
| Fundstelle: | Band 83, Jahrgang 1842, Nr. VIII., S. 37 |
| Download: | XML |
VIII.
Adcock's Wasserhebmaschine in der Kohlengrube bei Pemperton.Vergl. Polytechn. Journal Bd. LXXXII. S.
87.
Aus dem Mechanics' Magazine. Jul. 1841,S.
4.
Mit einer Abbildung auf Tab. I.
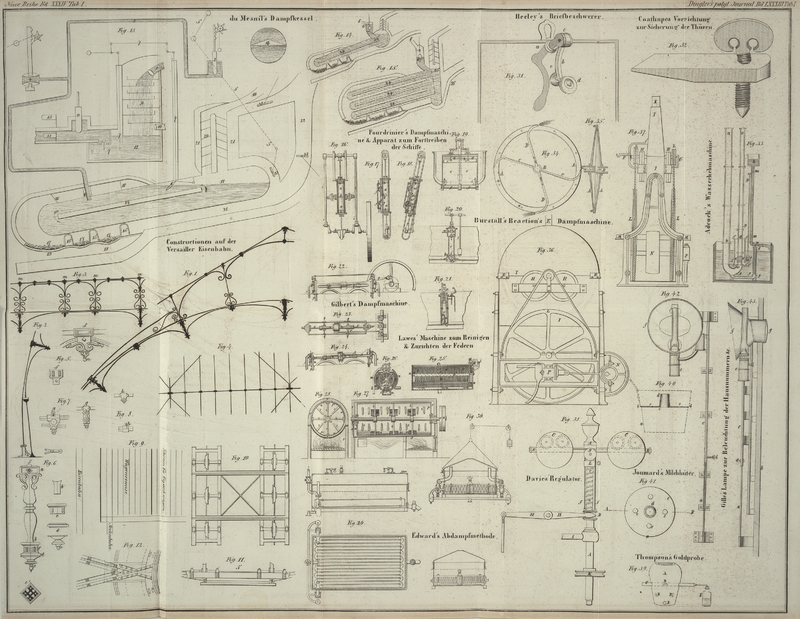
Adcock's Wasserhebmaschine.
Fig. 33 dient
zur Erläuterung einer für den 100 Yard tiefen Schacht bei Pemperton von mir
projectirten Einrichtung, um die Röhrenbiegung und den unteren Theil des Apparates
von allem Wasser zu befreien, welches sich aus irgend einer Veranlassung darin
angesammelt haben sollte.
a, b, c stellt einen Theil der abwärts führenden Röhre
oder derjenigen Röhre dar, welche die Luft von der Mündung des Schachtes durch die
gebogene Röhre in die aufwärtsführende Röhre leitet. b
ist die gebogene Röhre, welche auf dem Grunde des Schachtes die abwärtsführende
Röhre mit der aufwärtsgehenden verbindet. c, d, e ist
die zu Tage führende Röhre, durch welche die Luft mit Wasser vermengt oben zur
Schachtmündung gelangt, wo man das Wasser wieder in eine dichte Masse sich ansammeln
und von da frei ablaufen lassen kann. b, b sind fünf
Schlize, durch welche das Wasser, wenn der Apparat in Gang ist, aus einem an der
Sohle des Schachtes angelegten Sumpfe in die aufwärtsgehende Röhre fließt, um durch
den Luftstrom in Tropfen zertheilt gleichsam als Regentropfen zu Tage gefördert zu
werden. Die abwärtsgehende Röhre hält 29½ Zoll, die aufwärtsgehende
17½ Zoll im Durchmesser. Sind sie nicht in Thätigkeit und es rinnt aus irgend
einer Veranlassung Wasser aus dem Sumpfe in den Apparat, bis es sich darin auf
gleiche Höhe mit dem Wasserniveau des Sumpfes stellt, d. h. ungefähr auf 8′
über die tiefste Stelle der Röhrenbiegung oder 8′ 7″ über die tiefste
Stelle der unter dieser Röhrenbiegung befindlichen Röhre, so steigt das Wasser auch
in der Röhre g, g, g, g, deren Durchmesser 4 Zoll
beträgt, auf dieselbe Höhe. m, m ist eine 20 Fuß lange,
gleichfalls 4 Zoll im Durchmesser haltende Rohre, welche von einem Wasserbehälter
oder einer Rinne h aus mit Wasser gespeist wird. Dieser
Behälter ist so angeordnet, daß er das durchsikernde und zu den Seiten des Schachtes
hinabrieselnde Wasser auffängt. Die Röhre m, m endigt
sich in einen doppelt
konischen Ansaz n. Die Dimensionen des kleineren Kegels
sind folgende: sein größter Durchmesser ist 96/100 Zoll, sein kleinster 6/10 Zoll,
seine Länge ½ Zoll; der kleinste Durchmesser des größeren Kegels ist 6/10
Zoll, der größte 1 1/12 Zoll, seine Länge beträgt 5 4/10 Zoll. Von der
Vereinigungsstelle des größeren Kegels mit dem kleineren steigt eine 6/10 Zoll dike
Röhre in die 4zöllige Röhre g, g, g, g herab. Diese
Röhre ist 9 Fuß lang.
Nach dieser Angabe der Verhältnisse gehe ich nun zur näheren Untersuchung der
Vorrichtung über. Das Wasser in der Röhre m, m wird
durch den Wasserbehälter oder das die Seiten des Schachtes hinabrieselnde Wasser auf
einer Höhe gleich der Höhe der Röhre selbst, nämlich 20 Fuß, erhalten. Nun ist es
bekannt, daß die theoretische Geschwindigkeit des aus einer Oeffnung fließenden
Wassers gleich ist der Geschwindigkeit eines von der Höhe des Wasserniveau's
herabfallenden schweren Körpers, und diese wird in Fußen per Secunde ganz genau gefunden, indem man die Quadratwurzel aus der
Fallhöhe mit 8 multiplicirt. Demnach liefert eine Fallhöhe von 1 Fuß eine
Geschwindigkeit von 8, eine Fallhöhe von 9 Fuß eine Geschwindigkeit von 24 Fuß, und
eine Fallhöhe von 20 Fuß eine Geschwindigkeit von 35¾ Fuß in der Secunde.
Dieß ist die theoretische Geschwindigkeit. Nun ist aber bekannt, daß Wasserstrahlen
beim Ausströmen durch Mündungen einer Contraction unterliegen; wir müssen daher, um
die wirkliche Ausflußgeschwindigkeit zu finden, die Quadratwurzel aus der Höhe mit 5
anstatt mit 8 multipliren. Nach Versuchen von Venturi, Bryan,
Donkin und anderen ist ferner bekannt, daß wenn Wasser durch einen
konischen Ansaz fließt, die Ausflußmenge, mithin auch ihre Geschwindigkeit an der
Verengung, sogar größer als die aus der Theorie abgeleitete Geschwindigkeit ist. Da
jedoch die 20′ hohe Röhre gerade vor ihrer Vereinigung mit dem
doppeltkonischen Ansaz in eine Biegung ausgeht, so will ich zur Vermeidung von
Einwürfen die Geschwindigkeit des durch den konischen Ansaz fließenden Wassers so
annehmen, wie sie sich aus der Contraction des Wasserstrahls ergibt. Ich seze also 5
√20 = 22½ Fuß anstatt obiger 35 ¾ Fuß.
Ich habe oben bereits bemerkt, daß der Durchmesser der 9 Fuß langen Saugröhre, welche
von dem engeren Theil des doppelten konischen Ansazes in die Röhre g, g, g, g hinab sich erstrekt, 6/10 Zoll beträgt. Da
nun die Geschwindigkeit des an ihrer Verbindungsstelle mit dem konischen Ansaz über
derselben hinwegfließenden Wassers 22 Fuß in der Secunde ist, so beträgt die Zeit,
welche verfließt während
ein Wassertheilchen über den Durchmesser der erwähnten Röhre sich bewegt, 1/440
Secunde = 0,00227 Secunden.
Nun findet man nach den Gesezen der Schwere den Raum, durch welchen ein Körper in
einer gegebenen Zeit fällt, in Fußen, wenn man das Quadrat der Zeit, in Secunden
ausgedrükt, mit 16 1/12 multiplicirt.Die Zahl 16 1/12 bezeichnet den von einem frei fallenden Koͤrper in
der ersten Secunde zurükgelegten Raum in englischen Fußen; nach Pariser Maaß
betraͤgt derselbe 15.1, nach rheinlaͤndischem 15,625 Fuß.Der Uebers. Es ist
demnach in Zollen ausgedrükt sehr nahe:
0,002272 × 16 1/12
× 12 = 0,001 Zoll.
Zieht man außer den Gesezen der Schwere auch noch die Erweiterung des äußeren Kegels
von 6/10 bis 1/12 Zoll, ferner den Umstand in Betracht, daß bei einer Länge von 5
4/10 Zoll während des Hinwegfließens des Wassers über die Mündung der 6/10 zölligen
Röhre kein Theilchen desselben Zeit hat in die Röhre hinabzufallen, so wird man
begreiflich finden, daß das mit großer Geschwindigkeit über diese Mündung
hinwegströmende Wasser vermöge seiner Friction, Adhäsion oder des Gesezes der
seitlichen Mittheilung der Bewegung bei Flüssigkeiten, zuerst einen Theil der Luft,
dann einen Theil des Wassers mit sich reißt, und dadurch ein theilweises Vacuum
veranlaßt. Jezt tritt das Gewicht der Atmosphäre in den beiden Röhrenleitungen in
Wirksamkeit und drükt das in denselben befindliche Wasser durch die Röhre g, g, g, g in ununterbrochenem Strome so lange in die
6/10 zöllige Röhre hinauf und von dieser in den weiteren Kegel, bis das Wasserniveau
in der Röhrenbiegung unter den tiefsten Punkt derselben gesunken ist.
Auf solche Weise löse ich diese wichtige Aufgabe ohne Ventile, Klappen, Pumpen oder
sonstige Vorrichtungen, welche möglicherweise in Unordnung gerathen können.
Tafeln