| Titel: | Beiträge zur Geschichte, Theorie und Praxis der Zeicheninstrumente, insbesondere der Ellipsographen; von Prof. Ernst Fischer. |
| Autor: | Ernst Fischer |
| Fundstelle: | Band 255, Jahrgang 1885, S. 261 |
| Download: | XML |
Beiträge zur Geschichte, Theorie und Praxis der
Zeicheninstrumente, insbesondere der Ellipsographen; von Prof. Ernst
Fischer.
(Schluſs der Abhandlung S. 217 d. Bd.)
Mit Abbildungen auf Tafel
14 und 20.
Ernst Fischer, über Zeicheninstrumente.
Der bereits in der Zeitschrift für Vermessungswesen,
1876 S. 459 von Jordan erwähnte Centrograph, welchen der Mechaniker Stanley
in London ausgestellt hatte, gestattet die Beschreibung von Kreisbögen dadurch, daſs
der Zeichenstift im Scheitel eines Winkels sitzt, dessen Schenkel an zwei gegebenen
Punkten des Kreisbogens, welche durch die Kanten schwerer Gewichte festgelegt sind,
vorüber geführt werden. Im Vergleiche zu dem vorher besprochenen Curvenlineal dürfte
eine geringere Bequemlichkeit wohl entschieden hervortreten; dagegen ist der Apparat
Stanley's aber voraussichtlich wohlfeiler, weil
leichter den mathematischen Anforderungen entsprechend herzustellen.
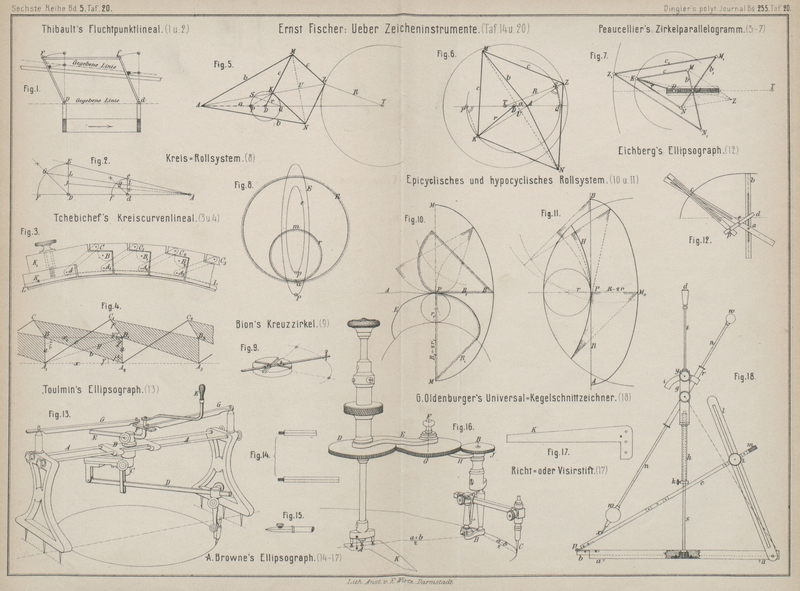
Am meisten empfehlenswerth zur Construction ist aber das Zirkelparallelogramm von Peaucellier, ein
Apparat, welcher seit einigen Jahren die Aufmerksamkeit auf sich gezogen hat, obzwar
derselbe bereits vor etwa 20 Jahren erfunden wurde, aber allgemeine Beachtung erst
dann fand, als sich zu Anfang des vorigen Jahrzehnts die Erfindung in Ruſsland
wiederholte und ihre Wichtigkeit für die praktische Mechanik von Fachmännern (und
zwar besonders von Seiten Tchebicheff's) erkannt worden
war. Das Zirkelparallelogramm wird in verschiedenen Formen angewendet: Fig. 5 und 6 Taf. 20
zeigen in den starken Linien die ursprünglichen Formen, Fig. 7 eine andere, welche
auf der Londoner Ausstellung durch ein Modell vertreten war. Andere Formen sind dem
Apparate von Hart und Kempe gegeben worden; sie werden
als hier weniger wichtig übergangen.
Wir beginnen die nähere Erklärung mit Bezug auf Fig. 5 Taf. 20. A und D sind in der
Papierebene 2 feste Punkte, um welche sich die von den starken Linien gebildete
Figur dreht. KMZN ist ein Rhombus mit der Seitenlänge
c; seine Ecken werden von Gelenken gebildet und
zwei dieser Ecken, M und N, haben von A den gleichen Abstand b. Die Ecke K beschreibt
um D einen Kreisbogen vom Radius r.
Nun ist erstens ersichtlich, daſs
immer die 3 Punkte A, K und Z auf einer Geraden liegen, was wohl keines Beweises bedarf. Ferner ist
zweitens AK × AZ eine
Constante. Man hat:
\overline{M\,U^2}=b^2-1/4\,(A\,Z+A\,K)^2, andererseits:
\overline{M\,U^2}=c^2-1/4\,(A\,Z-A\,K)^2,
daher durch Subtraction:
AK\times AZ=b^2-c^2 . . . . . . . . . .
(1)
Daſs auch Z in Folge dieser eben
angegebenen Beziehungen einen Kreis beschreibt, ist aus folgender Betrachtung zu
erkennen: Die Linie AKZ schneidet den von K um D mit dem Radius r beschriebenen Kreis auſser in K auch in S. In Folge der Aehnlichkeit der
Dreiecke ASQ und AKP hat
man die bekannte Relation: AS × AK = AP × AQ. Setzt man
nun, wie in Fig.
5 angegeben, AD = a, so wird hiermit, weil
AQ = a + r und AP = a –
r ist:
AS\times AK=a^2-r^2, also in Verbindung
mit (1)
\frac{A\,Z}{A\,S}=\frac{b^2-c^2}{a^2-r^2} . . . . . . . . .
. (2)
Weil aber zufolge dieser Gleichung AZ und AS für beliebige
Lagen in constantem Verhältnisse stehen, so beschreiben S und Z ähnliche Figuren, deren
Aehnlichkeitspunkt A ist. Man erkennt, daſs Z in der That einen Kreis beschreibt, dessen Radius R mit Rücksicht auf das Verhältniſs der Abmessungen der
ähnlichen Figuren, welches aus der Gleichung (2) sich ergibt, gleich ist:
R=r\,\frac{b^2-c^2}{a^2-r^2} . . . . .
. . . . . (3)
Fig. 5 bezieht
sich auf den Fall b > c, a
> r; jedoch ist die Gültigkeit der Entwicklung nicht
davon abhängig, daſs diese Ungleichungen erfüllt sind, wenn man negative Strecken
zuläſst. Ist a < r, so liegt der
Aehnlichkeitspunkt A im Inneren der Kreise und R wird dem entsprechend von Formel (3) negativ
angegeben, indem es eben in der That eine wesentlich entgegengesetzte Richtung
erhält.
Fig. 6 bezieht
sich auf den Fall b < c und a < r und auch hierfür gelten
dieselben Formeln. Die Bezeichnungen in dieser Abbildung sind dieselben wie in Fig. 5, so daſs
es nicht schwer hält, die Richtigkeit der obigen Entwickelung auch für diese Annahme
festzustellen.
a = r gibt in beiden Fällen R = ∞, d.h. der Punkt Z
beschreibt alsdann eine Gerade, eine Eigenschaft des Apparates, die sich namentlich
für den Maschinenbau sehr nützlich erweist (vgl. Peaucellier's Geradführung 1875 217 * 362).
Betrachten wir nun Fig. 7 Taf. 20, so besteht
anscheinend eine wesentliche Abweichung gegen Fig. 5 und 6. Allein wenn man KMN durch die punktirten Linien MZ und NZ zu einem Rhombus KMZN ergänzt, springt die Aehnlichkeit mit Fig. 6 in die
Augen. Der Punkt Z würde einen zu dem von K beschriebenen ähnlichen Kreis beschreiben,
desgleichen Z1, wenn
nur Viereck Z1M1AN1 ∾ ZMAN ist, wozu gehört, daſs c1 : c = b1 : b. Bezeichnen wir das Verhältniſs mit v, so ist also:
c_1:c=b_1:b=v, sowie
AZ_1:AZ=v . . . . . . . . . . (4)
In Fig. 7 ist v = 2. Die Formeln (1) und (3),
in denen anstatt b2 –
c2 jetzt wegen
c > b besser c2 – b2 zu schreiben ist, was nur auf das Vorzeichen der
Strecken Einfluſs hat, geben durch Einführung der Relation (4): AK × AZ1 = (c1 + b1) (c – b) = s1d und daraus:
R=r\,\frac{(c_1+b_1)\,(c-b)}{r^2-a^2}=r\,\frac{s_1\,d}{r^2-a^2},
. . . . . . . . . . (5)
worin s1 und d Abkürzungen für
„Summe“ und „Differenz“ bedeuten.
In ähnlicher Weise, wie Fig. 7 als eine Abänderung
der Fig. 6
betrachtet werden kann, ist es möglich, auch Fig. 5 umzustellen
u.s.w.
Wenden wir uns nun näher zur Ausführung
eines Zirkels nach Fig. 7 Taf. 20, so ist
zunächst ersichtlich, daſs die Drehpunkte A und D sich auf einer Platte (dem Fuſse des Zirkels)
befinden müssen, daſs zur Veränderung des Abstandes AD
= a für A eine
Schlittenführung eingerichtet und daſs endlich damit eine mikrometrische Bewegung
zur feinen Einstellung bestimmter a verbunden sein
muſs. Das Gelenk Z1
kann mit Bleistift- oder Reiſsfedereinsatz versehen werden.
In der Wahl der Abmessungen besteht, wie es beim ersten Blicke auf
den Ausdruck von R den Anschein hat, eine groſse
Freiheit, weil sehr verschiedene Werthsysteme r, (c1 + b1), (c – b) und a dasselbe R berechnen lassen. Da aber zwischen jenen Gröſsen aus
der Figur zu entnehmende Bedingungen bestehen, so wird die Amplitude der möglichen
R beschränkt sein. Wird man nun derjenigen
Construction den Vorzug geben, welche diese Amplitude am gröſsten hat, so ist doch
nächstdem noch besonders die mögliche Länge der zu beschreibenden Bögen von
Wichtigkeit. Mit Rücksicht hierauf leiten wir die geometrischen Bedingungen der
Construction im Folgenden ab:
Eine erste Bedingungsgleichung folgt aus der Einführung des
kleinsten möglichen R bei r > a in die Formel (5). R0 bezeichne das
kleinste R für r > a, so ist:
R_0=r\,\frac{s_1\,d}{r^2-{a_0}^2}, . .
. . . . . . . . (6)
worin a0 der kleinste mögliche a-Werth ist. a0 kann deshalb nicht Null sein, weil A und
D sich nicht als mathematische Punkte ausführen
lassen und man von einer Anordnung beider Drehpunkte über einander der
Umständlichkeit halber absehen wird. Auſser dieser Bedingung für a0 besteht noch die
geometrische:
r +a_0\geq d, . . . . . . . . . .
(7)
wie ein Blick auf Dreieck KMA lehrt, wenn man zugleich beachtet, daſs c –
b = d und bei gegebenem r und a0 der gröſste Werth der Seite KA = r + a0 ist.
Ob es möglich ist, von derjenigen Stellung Nutzen zu ziehen, bei
welcher r + a0 = d, also der Zirkel
zusammengeklappt ist, hängt von der Anordnung und Gestalt der Schienen ab. Wir
wollen diese Möglichkeit voraussetzen.
Denken wir uns nun a wachsend, so
wird R ebenfalls gröſser werden. Da man aber den
Apparat besonders für flache Bögen nöthig hat, so muſs a jedenfalls sehr nahe gleich r oder besser
gleich r werden können, wofür R = ∞ ist. Wächst a weiter, so nimmt R wieder ab, die Bögen werden convex und schlieſslich
wird ein zweiter Mindestwerth von R erreicht werden. In
dieser Weise kommen wir, wenn das kleinste R für a > r mit Rm bezeichnet wird, zu der Bedingung:
R_m=r\,\frac{s_1\,d}{{a_m}^2-r^2}, . .
. . . . . . . . (8)
worin am der gröſste mögliche a-Werth. Hierzu gesellt sich die geometrische Bedingung:
r+a_m\,\leq\,\frac{s_1}{v}, . . . . . .
. . . . (9)
indem im Dreiecke KMA
jederzeit KA nicht gröſser als c + b sein kann. Eine weitere Bedingung folgt
daraus, daſs zur Bequemlichkeit der Construction und der Handhabung des
Zeichenstiftes der Punkt Z1 auſserhalb AK liegen muſs. Die Entwickelung
zur Gleichung (5) gibt AZ1 = s1d : AK und, setzt man den
Ausdruck rechter Hand gröſser als AK, so wird:
A\,K\,<\,\sqrt{S_1\,d}.
Nun ist der gröſste Werth von AK
gleich r + am; man erhält damit die Bedingung:
r+a_m\,<\,\sqrt{s_1\,d} . . . .
. . . . . . (10)
Man bemerkt leicht, daſs vorstehende Entwickelung unmittelbar für
Fig. 7
gilt, wenn man v = 1 annimmt; nur fällt die Gleichung
(9) ganz weg. Bei der Anwendung der Formeln auf Fig. 5 ist auch v = 1 zu setzen, die Gleichung (9) aber beizubehalten,
da dieselbe die Bedingung ausdrückt, daſs eben AK <
AZ bleiben muſs.
Zu diesen Bedingungen treten nun die Ausdrücke, welche die
Bogenlänge charakterisiren. Denkt man sich Z1 in Bewegung, so nimmt AK fortwährend ab, wenn man mit der dem Falle AK =
a + r entsprechenden Lage beginnt. Die Bewegung von Z1 läſst sich beiderseits dieser
Anfangslage fortsetzen, bis AK = c – b = d wird; alsdann ist der Zirkel wieder zusammengeklappt.
Die Länge von AZ1 ist
alsdann c1 + b1 = s. Nun liegt der Centriwinkel des durch Z1 von der Anfangslage
aus beschriebenen Bogens in dem Dreiecke AZ1T, welches in Fig. 7 wegen
Mangel der Angabe des Kreismittelpunktes T nicht
sichtbar ist, an der Ecke T gegenüber der Seite AZ1 = s1. Die Nachbarseiten
sind TZ1 = R und TA = aR : r. Bezeichnet man diesen Winkel mit T, so ist nun nach einer bekannten trigonometrischen
Formel:
cos\,T=\frac{R^2+(a^2\,:\,r^2)\,R^2-{s_1}^2}{2\,(a\,:\,r)\,R^2}
wofür man entweder nach Multiplication mit r2 im Zähler und Nenner, oder unter Einsetzung von
Ausdruck (5) für R, erhält:
cos\,T=\frac{R^2\,(a^2+r^2)-r^2\,{s_1}^2}{2\,a\,r\,R^2}=\frac{(r^2+a^2)\,d^2-(r^2-a^2)^2}{2\,a\,r\,d^2}
. . . . . . . . . . (11)
Bildet man mittels des zweiten Werthes für cos T nach der Formel cos
T = 1 – 2sin 2½ T
den Werth für sin ½ T so
folgt ohne Rücksicht auf das Vorzeichen:
sin\,1/2\,T=\frac{r-a}{2\,\sqrt{a\,r}}\,\sqrt{\frac{(r+a)^2}{d^2}-1}
und
4\,R\,sin\,1/2\,T=2\,s_1\,\sqrt{\frac{r}{a}\,\left(1-\frac{d^2}{(r+a)^2}\right)}
. . . . . . . . . . (12)
Für sehr flache Bögen ist 4 R sin ½
T aber der ganzen von Z1 beschriebenen Bogenlänge nahezu gleich
und, da für solche auſserdem a nahezu = r ist, hat man die Länge flacher Bögen:
L=s_1\,\sqrt{4-(d^2\,:\,r^2)} . . . . .
. . . . . (13)
Andererseits hat man für R0, wenn r +
a0 = d ist, cos T = 1, T = 0 und also die Bogenlänge Null; jedoch wächst sie
mit wachsendem a0
ungemein rasch, weil der Differentialquotient nach a
von 4 R sin ½ T für r + a0
= d unendlich groſs ist.
Der Ausdruck für cos T zeigt, daſs
cos T = Null wird, also Halbkreise beschrieben werden für:
a^2=r^2+1/2\,d^2\,\pm\,\sqrt{2\,d^2\,(r^2+1/2\,d^2)} . . . .
. . . . . . (14)
Das obere Vorzeichen bezieht sich, weil es a > r gibt, auf convexe
Bögen; das untere Vorzeichen würde zu reellen a nur
führen, wenn r ≧ d
angenommen wäre; es entspricht, weil a < r wird,
concaven Bögen. Der Ausdruck für cos T zeigt ferner,
daſs Vollkreise beschrieben werden, also cos T = –1 ist, wenn:
a=r\pm d, . . . . . . . . . . (15)
worin das obere und untere Vorzeichen convexen bezieh.
concaven Bögen entsprechen. Vollkreise werden auch beschrieben, wenn:
a > r + d bei convexen bezieh.
a < r – d bei concaven Bögen (16)
ist, wie am einfachsten die Figur zeigt.
Mit Hilfe der im Vorhergehenden entwickelten Bedingungsgleichungen
und Ausdrücke läſst sich nun bereits ganz im Allgemeinen Einiges aufstellen, was bei
der Construction eines Zirkels nach Fig. 7 zu beachten ist. Es
sind dies folgende vier Sätze:
1) Die Formel (13) zeigt, daſs die Länge flacher Bögen von s1 = c1 + b1, also von der Gröſse
des Zirkels abhängt. War diese Beziehung selbstverständlich, so zeigt doch dieselbe
Formel ferner das nicht unmittelbar einleuchtende Ergebniſs:
2) Die Länge flacher Bögen nimmt zu, wenn r gegenüber d = c –
b wächst. Die Betrachtung von Formel (6) lehrt weiter:
3) Zugleich mit dem Anwachsen der Länge flacher Bögen in Folge
Anwachsens von r relativ zu d nimmt der Minimalradius R0 concaver Bögen ab. Dagegen folgt aus Formel (8) in
Verbindung mit (9) und (10):
4) Im gleichen Falle nimmt der Minimalradius Rm convexer Bögen
zu.
Hiernach ist es nicht zweckmäſsig, den Zirkel vorherrschend auf
convexe Bögen einzurichten. Man wird denselben vielmehr in
erster Linie für concave Bögen construiren und damit zugleich möglichst lange
flache Bögen erzielen. Um nun aber auch convexe Bögen in besonderen Fällen
construiren zu können, muſs r nötigenfalls veränderlich eingerichtet werden, was keine
Schwierigkeiten bedingt.
Zur Berechnung eines concaven Zirkels
hat man nach dem Vorigen folgende Relationen:
R_0=r\,\frac{s_1\,d}{r^2-{a_0}^2} . . .
. . . . . . . aus (6)
r+a_0\geq d . . . . . . . . . . aus
(7) 2\,r < (s_1:v) . . . . . . . . . . aus (9),
indem nämlich am mindestens etwas gröſser als r angenommen werden muſs; ferner ebenso:
2\,\,<\,\sqrt{s_1\,d} . . . . .
. . . . . aus (10) L=s_1\,\sqrt{4-(d^2\,:\,r^2)} . . . . . . .
. . . aus (13).
Setzt man dazu als Bedingung, daſs man mit R0 Halbkreise oder mehr bis zu Vollkreisen
beschreiben könne, so sind r und d so zu wählen, daſs a02 zwischen den
Grenzen liegt:
r^2+1/2\,d^2-\sqrt{2\,d^2\,(r^2+1/8\,d^2)}\,\geq\,{a_0}^2\,\geq\,(r-d)^2
. . . . . . . . . . aus (14) und (15).
Die Relationen für R0 und L geben nach
Elimination von s1:
d=2\,r\,:\,\sqrt{1+\frac{L^2}{{R_0}^2}\,:\,\left(1-\frac{{a_0}^2}{r^2}\right)^2}
. . . . . . . . . . (17)
und ferner gibt die Relation für R0 mit der Beziehung
2\,<\,\sqrt{s_1\,d} in gleicher Weise: r2 (4r – R0) < –R0
a02. Da a0 jedenfalls klein ist, kann man rechts Null setzen
und hat dann sofort: 4r < R0.
Der Gang der Rechnung wird nun folgender: Man nimmt mehrere r nach Maſsgabe der Ungleichung 4r < R0, berechnet dazu die d
mittels der Gleichung (17), prüft die Befriedigung der Relation r + a0 ≧ d, sieht ferner zu, ob für R0 mindestens Halbkreise beschrieben
werden und berechnet nun s1 aus der Gleichung (13) und v < (s1 : 2r).
Beispiel: Gegeben L = 600mm, R0 = 300, a0 = 10. Es wird also
r < 75; wir nehmen hier sofort r = 70, da kleinere r, wie
sich zeigt, für kleine R eine kleinere Bogenlänge
ergeben. Weiter ist nun d=140\,:\,\sqrt{1+4\,:\,(1-1/49)^2},
welcher Werth kleiner als 75 + 10 ist, wie es sein soll. Die Substitution der Werthe
von r und d in die nächste
der oben aufgeführten Ungleichungen ergibt:
4900+1897-\sqrt{7589\,(4900+474)}\,\geq\,100\,\geq\,71. Da
der Ausdruck linker Hand sich auf 410 reducirt, so erhellt, daſs mit dem Radius 300
zwar nicht Vollkreise, aber doch weit mehr als Halbkreise beschrieben werden können.
Die genauere Rechnung gibt 280° Centriwinkel und 1465 Bogenlänge. Weiter ist
S_1=600\,:\,\sqrt{4-(61,6\,:\,70)^2}=334,0 und v
< (334,0:140).
Zur Berechnung eines convexen Zirkels
hat man folgende Relationen:
Weil r jedenfalls etwas gröſser als
a0 anzunehmen ist,
damit ganz flache Bögen bequem ohne Rücksicht auf ihre Krümmung zu beschreiben sind,
hat man: r > a0 und 2r > d aus Formel
(7). Ferner wird:
R_m=r\,\frac{s_1\,d}{{a_m}^2-r^2} . . .
. . . . . . . aus (8) r+a_m\,\leq\,\frac{s_1}{v} . . . . . . .
. . . aus (9),
r+a_m\,<\,\sqrt{s_1\,d} . . . .
. . . . . . aus (10) L=s_1\,\sqrt{4-(d^2\,:\,r^2)} . . . . . .
. . . . aus (13).
Als Bedingung, daſs Halbkreise bis Vollkreise von Rm beschrieben werden
können, hat man:
r^2+1/2\,d^2+\sqrt{2\,d^2\,(r^2+1/8\,d^2)}\,\leq\,a\,m^2\,\leq\,(r+d)^2.
Gegeben sind auch jetzt in der Regel L und Rm; die anderen Gröſsen sind zu wählen. Da jedoch der
früher berechnete concave Zirkel durch geändertes r
zugleich als convexer Zirkel gebraucht werden soll, so sind demnach bereits s1 und d gegeben, v aber noch
nach Maſsgabe einer Ungleichung zu wählen.
Beispiel. Es war: d = 61,6, s1 = 334,0 und v
< (334,0:140). Die ersten der obigen Ungleichungen führten zu r > 31. Wir nehmen r = 35.
Gröſsere r würden Rm stark vergröſsern, ohne auch L wesentlich zu vergröſsern. Es wird nun ferner:
35+a_m\,<\,\sqrt{334,0\,\times\,61,6}, d. i.
134,4
und am kann hiernach 100 noch überschreiten. Für am = 100 werden, da 100 > 35 + 61,6 ist,
noch Vollkreise beschrieben – auch gerade noch bei a =
96,6 mit R = 89. Für v
wird erhalten: v < (334,0:135).
Wir setzen v = 2, welcher Werth
theilweise geringere Maſse gibt als v = 1 und damit dem
Zirkel ein schlankeres Ansehen verleiht. Man hat nun:
s = 167,0 = c + b. c = 114,3. b =
52,7.
d = 61,6 = c – b. c1 = 228,6. b1 = 105,4.
L reducirt sich stark
gegen den früheren Werth; es wird etwas über 310.
Wir vergleichen nun die Construction nach Fig. 7 Taf. 20 mit einer
solchen nach Fig.
5. Nimmt man hier wie im Beispielsfalle s =
b + c = 334,0 und d = b – c = 61,6, so erhält man einen Zirkel, der gewiſs ebenso
brauchbar als derjenige nach Fig. 7 ist. Wollte man
aber bei Fig.
7 die Bedingung, daſs AZ1
< AK sein soll, weglassen, so würde Fig. 7 im
Vortheile sein; denn bei Fig. 5 kann diese
Bedingung nicht wegbleiben, weil die Lage von Z
unbestimmt wird, sobald K durch U hindurchgeht. Bei Fig. 6 ist von der eben
erwähnten Bedingung überhaupt nicht die Rede. Scheut man etwas gröſsere Breite des
Zirkels nicht, so ist die Construction nach Fig. 6 zu
empfehlen. Wir wollen dieselbe noch etwas eingehender betrachten.
Faſst man wieder zuerst concave Bögen ins Auge, so sind die
Relationen zu beachten:
R_0=r\,\frac{s\,d}{r^2{a_0}^2} . . . .
. . . . . . aus (6) r+a_0\geq d . . . . . . . . . . aus
(7)
2\,r < s . . . . aus (9)
L=s\,\sqrt{4-(d^2\,:\,r^2)} . . . . . . aus (13)
r^2+1/2\,d^2-\sqrt{2\,d^2\,(r^2+1/8\,d^2)}\,\geq\,{a_0}^2\,\geq\,(r^2-d^2)
. . . . . . . . . . aus (14) und (15).
Die Formeln für R0 und L geben wie
früher unter (17):
d=2\,r\,:\,\sqrt{1+\frac{L^2}{{}R_0^2}\,:\,\left(1-\frac{{}a_0^2}{r^2}\right)^2}
Führt man die Beziehung 2r <
s in R0 ein, so folgt mit Rücksicht auf den kleinen Betrag
von a0 die Beziehung
d < ½R0. Da nun sehr nahe
d=2\,r\,:\,\sqrt{1+(L^2\,:\,{R_0}^2)} ist, so hat man
r\,<\,1/4\,R_0\,\sqrt{1+(L^2\,:\,{R_0}^2)}. Hieraus
folgt vorerst r; dann berechnet man aus der eben
aufgeführten Gleichung (17) den Werth d und
schlieſslich aus s=L\,:\,\sqrt{4-(d^2\,:\,r^2)} den Werth s. Letztere beiden Werthe sind für nicht zu kleine r vom Betrage desselben nahezu unabhängig. Bestimmend
für die Wahl von r wird daher nur die Länge der Bögen
für kleine Radien und hier wird r möglichst groſs
gefordert. Wünscht man für R0 geradezu Vollkreise, so ist zu setzen: a0
= r – d, d.h.
r=a_0\,:\,\left(1-\frac{2}{\sqrt{1+(L^2\,:\,{R_0}^2)}}\right)
Ist es nach der obigen Ungleichung für r zulässig, r noch gröſser als nach der
letzten Gleichung anzunehmen, vermeidet man dies aber als überflüssig, so kommt es
nun den convexen Bögen zu Gute.
Beispiel. Gegeben: L = 600mm, R0 = 300, a0 = 10. Es wird
r\,<\,75\,\sqrt{1+4}, d. i. 168; dagegen
r=10\,:\,(1-2\,:\,\sqrt{1+4}), d. i. 95. Nehmen wir daher
rund r = 100, so erhalten die Bögen mit kleinen Radien
jede wünschenswerthe Länge. Es wird nun:
d=200\,:\,\sqrt{1+4\,:\,0,99^2}=88,7. s=600\,:\,\sqrt{4-0,887^2}=334,7.
c=211,7. b=123,0.
Nach Formel (9) kann als gröſstes a
erhalten werden: 334,7 – 100, d. i. 234,7. Hierfür ist:
R_m=100\,\frac{334,7\,\times\,88,7}{234,7^2-100^2}=66.
Nicht nur für dieses, sondern auch für noch gröſsere R werden Vollkreise beschrieben, so lange nämlich a ≧ 100 + 88,7. Zu a =
188,7 gehört R = 116.
Zur Erleichterung der Uebersicht über die Wirksamkeit des Zirkels
hat Helmert folgende Tabelle berechnet:
a
R
Centriwinkel
Bogenlänge
10 11,3
300 301
360°
–
18851890
38,9
350
144°
38'
883
50,8
400
113°
26'
792
63,7
500
82°
32'
720
83,8
1000
36°
52'
643
100
∞
–
0'
600
113,9
1000
32°
54'
574
126,3
500
63°
38'
555
141,1
300
103°
6'
540
157,6
200
155°
0'
541
163,9
176
177°
38'
546
167,3
165
190°
54'
550
172,6
150
213°
47'
560
180,3
132
254°
34'
587
188,7234,7
116 66
360°
–
729 415
Der Umfang der Wirksamkeit für convexe R ist hier so bedeutend, daſs es überflüssig wäre, noch ein zweites,
kleines r dem Apparate beizufügen.
Wir haben nunmehr sämmtliche Apparate aufgeführt, welche zur Herstellung von geraden
Linien und Kreisen dienen, und wir könnten eigentlich damit unsere Betrachtungen
schlieſsen; denn geometrische Zeichnungen bestehen zum gröſsten Theile aus geraden
Linien und Kreisen. Dieselbe Beschränkung kann man bei allen gewöhnlichen
Constructionen der
theoretischen Geometrie wahrnehmen. Es ist nachgewiesen worden, daſs jedes Problem,
welches nur eine einzige Lösung zuläſst, sobald die
nothigen Maſse graphisch gegeben sind, mit dem Lineale allein gelöst werden kann,
d.h. allein durch Zeichnung von geraden Linien ohne Anwendung des Zirkels, und daſs
jegliche Aufgabe quadratischer Natur, d.h. eine solche,
bei welcher zwei, aber nicht mehr Lösungen möglich
sind, mit Hilfe von Lineal und Zirkel gelöst werden kann.
Diese Bemerkungen werden vielleicht genügen, um darzuthun, daſs in der theoretischen
Geometrie die Wichtigkeit der geraden Linie und des Kreises weit überwiegend ist.
Auf der anderen Seite besitzen die gerade Linie und der Kreis eine Eigenschaft
gemeinsam, welche denselben unter allen ebenen Curven eigentümlich und welche für
alle praktischen Anwendungen der Geometrie unschätzbar ist: sie sind die einzigen in
derselben Ebene liegenden (oder nicht gefalteten) Linien, voll denen jeder beliebige
Theil jedem anderen genau angepaſst werden kann. In sehr vielen mechanischen
Einrichtungen ist diese Eigenthümlichkeit unentbehrlich und sie ist in allen Fällen
von Vortheil, in welchen Genauigkeit der Form erfordert wird; denn sie bietet ein
einfaches Mittel dar, um festzustellen, daſs Genauigkeit erzielt worden ist. Es gibt
nur eine gefaltete Curve, welche dieselbe Eigenschaft zeigt, nämlich die Schraubenlinie, und gerade weil bei ihr ebenfalls ein
jeder Theil von einem anderen gedeckt werden kann, wird die Einrichtung von Schraube
und Mutter möglich, weshalb diese Curve für die Mechanik von so groſsem Nutzen
ist.
Ungeachtet dieser Vorzüge der geraden Linie und des Kreises ist es doch gelegentlich,
sowohl in der theoretischen wie angewandten Geometrie, unumgänglich, auch andere
Curven zu ziehen. Es ist durchaus nicht eine leichte Sache, gute Methoden zur
Verzeichnung von Curven aufzufinden. Selbst wenn die Theorie einer Curve ziemlich
genau bekannt ist, ist es oft unmöglich, auf Grund dieser Theorie eine Art
anzugeben, wie die Curve auf mechanischem Wege beschrieben werden könnte, und nicht
jede von der Theorie vorgeschlagene Methode muſs so beschaffen sein, daſs sie
praktisch genau arbeitet.
Unter allen Curven scheint nach dem Kreise die Ellipse
am einfachsten und leichtesten zu zeichnen zu seinVgl. die betreffenden Zeichnungen in Ernst Fischer:
Vorlegeblätter zum Linearzeichnen. 3 Hefte mit je 12 Tafeln in
Farbendruck, nebst Text. (München 1876.); aber einige Autoritäten
in diesem Fache empfehlen dem Zeichner nicht, den Versuch zu machen, eine wahre
Ellipse herzustellen, sondern eine Nachahmung von einer Ellipse aus 6 bis 7
Kreisbögen, deren Mittelpunkte und Radien in geeigneter Weise gewählt worden sind,
zusammenzusetzen. Man sagt, daſs eine solche Nachahmung selbst ein wohlgeübtes Auge
befriedigt, obgleich es offenbar ist, daſs, während die Krümmung einer Ellipse sich
beständig ändert, die
Krümmung der nachgeahmten Curve in den Punkten, in denen die Kreisbögen
zusammentreffen, plötzlich wechselt. Peaucellier's
Gelenkverbindung, welche oben näher betrachtet wurde, mag vielleicht später diesen
Theil der Geometrie umgestalten. Schon weiſs man, daſs jeder Kegelschnitt und einige
der wichtigeren Curven 3. und 4. Grades durch Gelenkverbindungen oder
zusammengesetzte Zirkel, wie Peaucellier sie genannt
hat, verzeichnet werden können und daſs diese Vorrichtungen nicht zu umständlich
sind, um sicher zu arbeiten.
Die Ellipse ist nun in unseren graphischen Constructionen neben dem Kreise und den
cyclischen Curven wohl die am häufigsten vorkommende. Namentlich häufig in ihrer
Eigenschaft als schräge Projection des im Ingenieurbaue und in der Architektur ja so
unendlich häufig wiederkehrenden Kreises. Verleitet durch die leichten und hübschen
Verfahren zur Erzeugung von Kreislinien mittels des Zirkels, haben die Constructeure
sich immer wieder und wieder bemüht, sogen. Ellipsenzirkel – oder um den in diesem
Namen liegenden Widerspruch zu vermeiden – EllipsographenVgl. T. Rittershaus: Ueber Ellipsographen in den
Verhandlungen des Vereins zur Beförderung des
Gewerbefleißes, 1874 * S. 269 ff. zu erfinden, welche
für die Ellipse dasselbe leisten sollten, wie für den Kreis der Zirkel. Sie sind
sich dabei des prinzipiellen Unterschiedes, welcher in der Aufgabe gegenüber des
Verzeichnens eines Kreises liegt und der eine wirklich brauchbare Lösung fast
absolut unmöglich macht, selten oder nie bewuſst geworden. Sie haben sich durch das
stete Scheitern aller dieser Versuche durchaus nicht entmuthigen lassen, sondern den
schlechten Erfolg vielmehr stets auf Rechnung der nicht gelungenen Lösung
geschrieben. Ja, sie haben sich in den meisten Fällen nicht einmal bemüht, vorher in
der Literatur nachzusehen, ob nicht etwa ihre Idee bereits anderswo Fleisch und Bein
gewonnen. Deshalb begegnen wir in technischen Zeitschriften so häufig Constructionen
oder Vorschlägen für Ellipsographen, deren Zahl sich schon sicher nach Hunderten
beziffert; doch sind an wirklich verschiedenen Constructionen höchstens einige zehn
vorhanden, welche sich aber wieder ohne Ausnahme in 4 Hauptklassen eintheilen
lassen. Eine Unterordnung der verschiedenen Constructionen unter die allgemeinen
kinematischen Prinzipien haben wir Rittershaus in der
eben citirten Schrift zu verdanken und schlieſsen uns dessen Ausführungen hier an,
wobei auf die a. a. O. befindlichen Literaturnachweise, sowie auf dessen vorzügliche
Constructionszeichnungen verschiedener Ellipsographen besonders hingewiesen sei.
Wenn ein Kreis innerhalb eines anderen rollt, so beschreiben
sämmtliche Punkte des Rollkreises Hypocycloiden; ist der
Durchmesser des rollenden Kreises halb so groß als der des ruhenden, so gehen
sämmtliche Curven in Ellipsen überHierauf beruht ein Eilipsograph, welchen A.
Slaby in den Verhandlungen des Vereins zur
Beförderung des Gewerbefleißes, 1876 * S. 327 beschrieben
hat., und zwar speciell diejenigen der Umfangspunkte in Ellipsen mit
der kleinen Halbachse
Null, während die groſse Achse gleich dem Durchmesser des ruhenden Kreises wird und
mit diesem zusammenfällt (vgl. Fig. 8 Taf. 20). Ist R der ruhende Kreis, materiell aus einem Brette
geschnitten, so daſs in demselben der Kreis r von halb
so groſsem Durchmesser rollen kann, so beschreibt der innerhalb liegende Punkt p die Ellipse e, der
auſserhalb liegende P die Ellipse E; und zwar besitzt die erstere pm als groſse und pa als kleine, die letztere
Pm als groſse und Pa
als kleine Halbachse. Liegt der beschreibende Punkt also innerhalb des rollenden
Kreises, so ist die Summe der Halbachsen der erzeugten Ellipse = pa + pm gleich dem
Durchmesser des rollenden Kreises, liegt aber der beschreibende Punkt auſserhalb, =
Pm – Pa, also die Differenz der Halbachsen gleich
diesem Durchmesser. Auf diesem sehr bekannten Satze, mit dem sich zuerst der
Mathematiker Cardano beschäftigt hat und welcher daher
als das Problem der Cardani'schen Kreise bezeichnet
wird, beruhen fast neun Zehntel sämmtlicher Constructionen von Ellipsographen.
Dieselben sind aber in sehr verschiedener Weise zur Ausführung gebracht.
Eine namentlich sehr häufig wiederkehrende Form ist der sogen. Kreuzzirkel, zuerst von Bion im J. 1723 beschrieben, bei welchem, wie aus Fig. 9 Taf. 20 zu ersehen,
die Ellipse in der Weise erzeugt wird, daſs zwei Punkte einer Stange, welche auch
den beschreibenden Stift trägt, in – meist rechtwinklig – sich kreuzenden Geraden
geführt werden. Das Führungskreuz ist aus Holz oder Messing gefertigt und mit
kleinen Stiften versehen, mit welchen es auf das Papier festgelegt wird; in den
beiden Führungen gleiten kurze Pfannen, welche durch Zapfen mit zwei Schiebern
verbunden sind, die auf der Stange festgeklemmt werden. Groſse und Gestalt der zu
beschreibenden Ellipse ändern sich je nach der Entfernung der beiden geführten
Punkte und dieser vom beschreibenden Stifte und zwar sind die beiden letzteren
Gröſsen die Halbachsen.
Diese Grundconstruction ergibt sich aber aus dem Problem der Cardani'schen Kreise., indem daraus zu folgern ist:
1) Zwei Punkte einer Ebene bewegen sich auf den Schenkeln eines
Winkels, dessen Ebene mit jener zusammenfällt; irgend ein dritter Punkt der bewegten
Ebene beschreibt eine Ellipse.
2) Zwei Punkte einer Ebene bewegen sich der eine auf einem Kreise,
dessen Ebene mit der bewegten zusammenfällt und dessen Radius gleich dem Abstande
der beiden geführten Punkte, der andere Punkt auf einem Durchmesser dieses Kreises;
irgend ein dritter Punkt der bewegten Ebene beschreibt eine Ellipse.
3) Ein Kreis rollt in einem doppelt so groſsen; irgend ein Punkt
der Ebene des ersteren beschreibt eine Ellipse.
Die Zusammengehörigkeit dieser drei Fälle wurde bereits 1820 von
Jopling erkannt, welcher dieselben auch in
ähnlicher Weise neben einander stellte (vgl. Mechanics'
Magazine, 1820 S. 216).
Von allen drei Arten finden sich Beispiele und nicht etwa nur je
einzelne, sondern jedes in einer ganzen Reihe von constructiven Durchführungen.
Die Halbachsen der beschriebenen Ellipsen sind sofort immer zu
erkennen.
Für alle außerhalb des Rollkreises
liegenden Punkte haben die Halbachsen der Ellipse eine constante Differenz, für alle innerhalb
desselben liegenden Punkte eine constante Summe und
zwar beide Mal gleich dem Durchmesser dieses Kreises. Daraus folgt aber weiter, daſs
jeweilig congruente Ellipsen beschrieben werden von sämmtlichen Punkten eines zum
Rollkreise concentrischen Kreises. Es zerfällt also die ganze Ebene in concentrische
Kreise und die Punkte je eines solchen Kreises beschreiben congruente Ellipsen,
welche alle einen gemeinsamen Mittelpunkt haben.
Als Verallgemeinerung des zuerst angegebenen Satzes kann aber der
folgende gelten: Bewegen sich zwei Punkte einer Ebene auf zwei congruenten Ellipsen
mit gemeinsamem Mittelpunkte und ist die Entfernung jener Punkte gleich der Summe
(bezieh. Differenz) der Halbachsen, multiplicirt mit dem Sinus des Winkels, den die
groſsen Achsen mit einander bilden, so beschreibt irgend ein dritter Punkt der
bewegten Ebene eine Ellipse. – Mit den festen congruente Ellipsen werden beschrieben
von allen Punkten eines Kreises, dessen Durchmesser gleich der Summe der Halbachsen
ist. Wird die eine Halbachse Null, so geht der betreffende Kreis über in den rollenden
und die beiden Punkte bewegen sich auf Ellipsen mit der kleinen Halbachse Null und
der groſsen gleich dem Durchmesser des rollenden Kreises. Werden die Halbachsen
einander gleich, so schrumpft der Kreis in einen Punkt zusammen, den Mittelpunkt des
rollenden Kreises, und die einzig übrig bleibende Ellipse ist ein Kreis mit dem
Durchmesser gleich der Summe der Halbachsen.
Bisher waren beide Bahnen für die bewegten Punkte Kreise bezieh.
Ellipsen. Es gibt aber noch zwei Paare, welche ebenfalls charakteristische und –
wenigstens verhältniſsmäſsig – einfache Curven sind: Rollt nämlich eine Epicycloide oder eine Hypocycloide auf einer Geraden, so beschreibt jedesmal der Mittelpunkt des
Grundkreises eine Ellipse. Diese beiden Fälle sind in Fig. 10 und 11 Taf. 20
dargestellt. AB ist jedesmal die Gerade, auf welcher
die Cycloide rollt. Bewegt sich nun die Epicycloide E
in Fig. 10 so
durch den Punkt P, daſs sie in demselben beständig von
AB berührt wird, so beschreibt M, der Mittelpunkt des Grundkreises, die verzeichnete
Ellipse mit den Halbachsen R1 + 2r1 und
R1, wenn R1 lind r1 die Radien von
Grundkreis und Rollkreis bezeichnen. In Fig. 11 ist H die Hypocycloide und M0 beschreibt die Ellipse, R und R – 2r sind die Halbachsen.
Was nun die constructive Ausführung der Ellipsographen betrifft, so verweisen wir
zunächst auf die oben citirte Abhandlung von Rittershaus; im Uebrigen werden wir einige dort nicht betrachtete
Instrumente vorführen.
Interessant ist die Angabe von Eichberg (1852), den
Ellipsographen dazu dienstbar zu machen, beim Einwölben elliptischer Bögen, sowie
beim Vorzeichnen derselben auf dem Reiſsboden die genaue Form der Ellipse, zugleich
aber und namentlich auch die Richtung der Normalen, also die Richtung der Steinfuge zu geben.
Das Instrument besteht, dem Zwecke entsprechend, aus Latten mit
Drahtstiften. Die Nuth für den geführten Punkt a (Fig. 12 Taf.
20) ist an dem lothrechten Pfosten ab des Lehrgerüstes
oder, wenn hier kein Platz ist, am wagerechten Balken eingeschnitten. Die Normale
ist dadurch gegeben, daſs man eine Latte pc angebracht
hat, welche stets durch den beschreibenden Punkte und den Pol p geht. Es ist nämlich die Latte de, welche den einen
Punkt auf seinem Kreise führt, um ihre eigene Gröſse bis zum Pole verlängert (de = ep) und hier ist die die Normale vorstellende
Latte angeschlossen. Das Ganze ist recht einfach und jedenfalls sehr
zweckentsprechend und die sehr hübsche Idee, in der durch den Pol gehenden Stange
zugleich die Normale anzubringen, dürfte auch für andere Ellipsographen die
leichteste Lösung der Frage sein, wie die Ellipse mit der gewöhnlichen Ziehfeder,
welche bekanntlich stets tangential geführt werden muſs, auszuziehen sei.
Bemerkenswerth ist dann die Construction von HenryVgl. Annales des ponts et chaussées, 1872 S.
459., bei welcher, wie bei Eichberg
durch eine besondere Stange in jedem Augenblicke die Normale bestimmt wird. Dies ist
für den ganzen Apparat hier wesentlich; derselbe soll
nämlich weit weniger zur Zeichnung, als vielmehr zur
Ausmessung von Ellipsenbögen dienen (Appareil donnant le développement d'un arc quelconque
d'ellipse). Es ist daher statt des Bleies oder der Feder ein Meſsrädchen
angebracht; dasselbe muſs aber bei richtiger Messung stets tangential, d.h. mit
seiner Ebene senkrecht zur Normalen geführt werden, und dazu eben dient jene Stange.
Henry hat der Beschreibung seines Instrumentes
vortreffliche Zeichnungen beigegeben.
Die älteste Idee, Kegelschnittzeichner zu construiren,
dürfte wohl die sein, die Erzeugende des Kegels selbst die Zeichnung vollführen zu
lassen. In einer im J. 1821 erschienenen Schrift beschreibt der damalige
Superintendant Märtens zu Halberstadt ein von ihm
erfundenes Instrument, welches nach der eben angegebenen Idee ausgeführt, aber sehr
schwerfällig ist. Märtens beschreibt zunächst sehr
ergötzlich die Art, wie er durch die eigentümliche Gestalt des Schattens seiner
Studirlampe auf die Idee gekommen, seinen sogen. Conisector zu construiren. Märtens will
übrigens ganz richtig sein Instrument weit weniger als Zeicheninstrument betrachtet
wissen, als vielmehr als ein Unterrichtsmodell, um dem Schüler die Entstehung und
den Zusammenhang der Kegelschnitte anschaulich zu machen, und dazu ist dasselbe in
der That ebenso geeignet, wie das ihm nachgebildete von Oldenburger, welches weiter unten beschrieben wird.
Hier muſs zunächst noch eines Instrumentes gedacht werden, welches überall da recht
brauchbar ist, wo es sich weniger darum handelt, eine genaue Ellipse, als vielmehr
darum, eine Curve zu beschreiben, welche dem Auge als Ellipse erscheint, und dies
dürfte in allen graphischen Künsten die Regel sein. Wir meinen den so genannten
Ellipsograph von Davies. Derselbe ist einem
gewöhnlichen Zirkel sehr ähnlich; nur trägt der eine feste Fuſs eine um eine
wagerechte Achse drehbare Kreisscheibe, welche den zweiten Fuſs veranlaſst, an
derselben zu tangiren, folglich an der Berührungsstelle eine Ellipse, mit dem Stifte
oder der Feder aber eine der Ellipse parallele Curve zu beschreiben. Eine solche
Curve erscheint aber dem Auge nicht wesentlich verschieden von einer Ellipse und
kann dieselbe in den meisten Fällen ersetzen.
Es erübrigt uns nun nur noch einige gröſsere ausgeführte Constructionen zu
beschreiben, nämlich den Universal-Kegelschnittzeichner von Oldenburger, sowie die Ellipsographen von Toulmin und Browne.
Mit Hilfe des von G. Oldenburger in Bochum angegebenen
Apparates, Universal-Kegelschnittzeichner genannt,
sollen alle vier Kegelschnitte: Kreis, Ellipse, Parabel und Hyperbel, gezeichnet
werden können; derselbe soll vornehmlich als Anschauungsmittel beim Unterrichte
dienen. Seine Einrichtung Fig. 18 Taf. 20 beruht
darauf, daſs der Schreibstift auf dem Mantel eines Kegels geführt wird, während das
Zeichenbrett in den verschiedenen Neigungen zur Kegelachse, durch welche die Natur
des beschriebenen Kegelschnittes bedingt wird, festgestellt werden kann.
In dem Brettchen a befinden sich zwei
schwalbenschwanzförmig eingelassene Schieberlineale b,
an welchen das Zeichenbrett c durch Gelenke befestigt
ist. Mittels des Schieberlineals und der Gelenke kann dem Zeichenbrette c, das von m bis p geschlitzt ist, um bei seiner Drehung der Spindel s freien Durchgang zu gestatten, jede gewünschte Lage
gegeben werden; in der Figur 18 befindet sich
c in der Stellung für die Ellipse.
Das Zeichenbrett c wird durch zwei
geschlitzte Stützlatten l, welche mittels Schrauben z an c angedrückt werden,
in der gewünschten Lage erhalten. Auf dem Brettchen a
steht die Spindel s. welche die Kegelachse verkörpert
und um die sich die
Hülse h, gestützt durch den Klemmring k, drehen kann. Diese Hülse h bildet mit dem Gehänge g, der Stange t und dem Griffe d ein
Stück. Das Gehänge g trägt an zwei Zapfen das Rohr r, welches in der gegebenen Stellung durch den Bügel
i und die Klemmschraube y gehalten wird. In diesem Rohre kann sich die Schreibnadel n, die bei ihrer Drehung um die Achse s den ideellen Kegel beschreibt, in der Richtung der
Rohrachse frei bewegen. Die Schreibnadel ist durch kleine Gewichte w beschwert, welche den Schreibstift x fest auf die mit Papier besteckte Zeichenebene
drücken.
Wenn dem Kegel eine andere Gestalt gegeben werden soll, so braucht
man nur das Rohr r zu drehen oder den Klemmring k an einem höheren Punkte der Stange s festzuschrauben.
Vor dem Gebrauche des Apparates wird zuerst die Zeichenebene
gerichtet, dann die eine bezieh. die andere Seite des Zeichenbrettes c mit einem in der Mitte gelochten Papiere versehen, um
so über den Stift s gesteckt werden zu können,
schlieſslich der Klemmring k aufgeschoben und darauf
die Hülse h mit dem eigentlichen Schreibapparate
aufgesetzt.
Soll der – an einem Unterrichtsapparate wohl unerhebliche –
Uebelstand der Durchlochung des Papieres vermieden werden, so steht nichts entgegen,
die Hülse h, statt auf einer centralen Spindel, auf
einer weit gespreizten Gabel verschiebbar zu lagern, innerhalb welcher das
Zeichenbrett hinreichend Platz findet und die Drehung der Schreibnadel ungestört vor
sich gehen kann.
Mit Hilfe des in Fig. 13 Taf. 20 veranschaulichten Toulmin'schen EllipsographenVgl. Scientific American, 1875 Bd. 33 S.
230. lassen sich Ellipsen (mit der Kreisform beginnend bis zur
flachsten Ellipse) genau und schnell beschreiben.
A sind parallele Stangen, welche
einen Wagen B tragen; durch diesen geht die Hauptachse
C des Instrumentes, mit welcher der
Zeichenstiftträger D verbunden ist; der letztere trägt
verschiebbar den Bleistift oder die Reiſsfeder. Der Drehungsarm E geht durch den Kopf der Hauptachse und kann durch
eine Stellschraube in jeder beliebigen Lage gesichert werden. Auf den Drehungsarm
E ist der Kreuzkopf F
aufgesteckt; derselbe trägt die Bewegungsstangen G,
welche um fest auf den Gestellen angebrachte Nadeln drehbar sind. An den Gestellen
befinden sich Mittelpunktspitzen zum Aufstellen über jeder gewünschten Linie, in
welcher die kleine Achse der zu zeichnenden Ellipse liegen soll. Wie das Instrument
arbeitet, ist am besten aus der Abbildung zu ersehen.
Der in Fig. 14
bis 17 Taf.
20 abgebildete Ellipsograph von A. W. Browne in
Bloomfield, N. J.Vgl. Scientific American. 1873 Bd. 29 S.
22., beruht auf dem S. 268 entwickelten Prinzipe, nach welchem die
Ellipse sich als verlängerte bezieh. verkürzte Hypocycloide eines Rollkreises vom
halben Durchmesser des Grundkreises bildet.
Hiernach ist die Einrichtung dieses Apparates sofort verständlich.
Um das mit dem Stifte A festgehaltene Rad D werden die im Arme EH
gelagerten Planetenräder G und J herumgeführt. J hat halb so viel Zähne als
D, während die Zähnezahl von G, welches nur als Zwischenrad dient, beliebig ist. Es
wird sich demnach die Achse B bei jedem Umlaufe um A 2mal in entgegengesetzter Richtung umdrehen, mithin
dieselbe Bewegung ausführen wie der Mittelpunkt des in einem doppelt so groſsen
Grundkreise rollenden Rollkreises. Der mit dieser Achse in Verbindung gebrachte
Schreibstift C (oder Reiſsfeder Fig. 15) wird daher
jedenfalls eine Ellipse beschreiben, deren Achsenverhältniſs jeden Werth von Null
bis 1 annehmen, welche daher alle Formen zwischen Kreis und Gerade durchlaufen
kann.
Die Arme E und H sind durch ein Gelenk F
verbunden und können unter beliebigem Winkel gegen einander festgestellt werden,
womit sich dann der Abstand der Achse B vom
Mittelpunkte A verändern läſst. Ebenso kann der Arm des Schreibstiftes
C mit Hilfe der Einsatzstücke Fig. 14 verlängert und
verkürzt werden.
Wie aus der Theorie des Instrumentes sich sehr leicht ergibt, ist
der Radius AB gleich der halben Summe, der Radius BC gleich der halben Differenz der Halbachsen der zu
ziehenden Ellipse, wonach sich die Einstellung des Instrumentes leicht
bewerkstelligen läſst.
Mit diesem Instrumente ist man im Stande, Ellipsen von den
verschiedensten Achsenverhältnissen zu beschreiben (natürlich innerhalb gewisser
Grenzen, welche von dem Umfange bezieh. der Gröſse des Instrumentes abhängen) und
ebenso können die Hauptachsen auf jedem beliebigen rechtwinkeligen Geradenpaare
liegen.
Um das Instrument der Gröſse des Achsenpaares anzupassen, werden
die Längen der groſsen und der kleinen Achse addirt und die Summe durch 4 dividirt,
wodurch man den Abstand erhält, in welchem die Mittelpunkte A und B aufzustellen sind; die Länge der
kleinen Achse wird dann von der Länge der groſsen abgezogen und der erhaltene Rest
ebenfalls durch 4 dividirt, wodurch sich der Abstand ergibt, in welchem die
Bleistiftspitze von dem Centrum B sich zu befinden
hat.
Um eine bestimmte Ellipse, mit ihrer groſsen Achse auf einer
gegebenen Geraden liegend, zu beschreiben, wird der sogen. Richt- oder Visirstab K (Fig. 16 und 17) auf die 3
Spitzen des Instrumentenfuſses in A gesetzt, so daſs
die auf K und dem Fuſse angebrachten Sternchen
übereinstimmen. Das Centrum B und die Schreibspitze C werden beide an die Kante des Richtstabes gebracht
und die drei Punkte in A auf der gegebenen Geraden, zu
welcher die Kante des Richtstabes senkrecht ist, angemerkt. Der Richtstab wird dann
weggenommen und die Ellipse beschrieben.
Zum Schlusse fügen wir noch einige Literaturnachweise über Kegelschnittzeichner
an:
Robicek's Kegelschnittzeichner,
insbes. Parabolograph in D. p. J. 1830 38 * 81.
Thallmayer's Ellipsograph u. dgl.
1878 227 * 337. * 430. * 592. 228 * 106.
S. W. Balch's Eilipsograph im Scientific American, 1879 Bd. 41 * S. 324.
L. Bigge's bez. L. Abbot's Eilipsograph in D.
p. J. 1882 245 * 253 bez. 1885 255 * 20.
L. Burchard's Ellipsenzirkel in Carl's Repertorium, 1877
Bd. 13 * S. 528.
Drzewiecki's Kegelzirkel für die
direkte Construction der Kegelschnittslinien mit der Reiſsfeder; von M. Kuhn in Carl's Repertorium, 1874 Bd. 10 * S. 420.